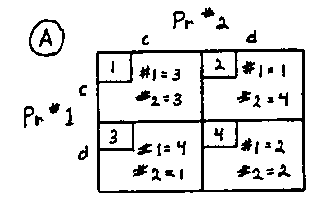
where:
"c" means to cooperate with the other prisoner and keep silent;
"d" means to defect and confess;
"#1=3" means that for prisoner #1, the utility of not confessing is 3;
"#2=4" means that for prisoner #2, the utility of defecting is 4, etc.
Contrary to what many people might expect, pacifism is compatible with the most modern branches of political science. This can be demonstrated by showing how "rational choice theory," "game theory," and probability analysis, three fields of political science theorizing, fit together to demonstrate that pacifism's the most reasonable and scientific approach to international relations.
Both rational choice and game theory are based on classical economic analysis, and make use of a concept called "utility." Utility is a way of expressing a person's degree of preference. For example, if a person prefers lentils to steak, would say that for that person,
lentils have more utility than steak. If we let UL represent the preference for the lentils, and US the preference for the steak, then the preference for the lentils over the steak can be expressed symbolically this way:
UL > US
Also, we can express the preference by assigning numbers to the preferences. For example, we could say that-the number 5 represents the person's preference for the lentils, and the number 3 the preference for the steak. This numerical way of comparing utilities can be tricky, for it tempts one to treat utilities as if they can be precisely measured, and manipulated in all the ways that mathematics manipulates numbers. Doing this doesn't always make sense. For our purposes, we'll limit the use of numbers to simply show that a person has one preference that's greater than another.
Rational choice theory tells us that a choice is always rational if a person, when comparing utilities, always chooses the higher utility. For example, if the person who likes lentils better than steak always chooses the lentils, then he or she is acting rationally. Choosing the steak over the lentils would be irrational. This definition of a rational choice must be modified by a notion of "reality." A mentally ill person might prefer to believe him or herself to be Napoleon rather than Julius Caesar, but because neither idea has a strong relationship to reality we wouldn't call it rational even if the person always tried to act like Napoleon.
Game theory is a branch of rational choice theory. Game theory has to do with situations in which a person's choices are reactions to what he or she thinks another person will do. A situation called "prisoners' dilemma" (pd) strikingly illustrates game theory, and is the subject of a great dealof modern political science theorizing.
In prisoner's dilemma, a district attorney has had arrested and imprisoned incommunicado in respect to each other two people suspected of conspiracy in a crime. The d.a. then goes to each prisoner, and offers him or her a "deal." If the prisoner confesses, he or she will receive a small sentence. If he or she doesn't confess,. and the d.a. wins the case, the d.a. will ask for the maximum sentence. The prisoners also know if that if neither of them confesses there's a good chance that they'll go free. What will each prisoner do? Each knows that if both keep quiet, if they "cooperate" with each other, they may go free. However, neither knows that the other will decide to do that. Both also know that if he or she decides to "defect" and confess, he or she probably will receive a short sentence. But both also know that if they don't confess, and the other does, he or she will receive the maximum sentence. It's to the self-interest of the two to cooperate with each other and not confess, but since neither knows what the other will do, the most rational course is to confess. Consequently, both defect and confess.
This situation can be symbolized by the following "matrix"

where:
"c" means to cooperate with the other prisoner and keep silent;
"d" means to defect and confess;
"#1=3" means that for prisoner #1, the utility of not confessing is 3;
"#2=4" means that for prisoner #2, the utility of defecting is 4, etc.
It's evident from this matrix that if both prisoners start in cell #1, they'll be tempted to migrate to cells #2 and #3. If both do this, then both will move next to cell #4.
Many political scientists believe that prisoners' dilemma can be used to symbolize the arms race between the United States and the Soviet Union. They interpret cell #1 as negotiated, multilateral disarmament, cells #2 and #3 as unilateral disarmament for one or the other nation, and cell #4 as continuing the arms race. In cell #4, the utility numbers represent the advantages of political freedom less the costs and dangers of the arms race.
Also, they believe that if pd is played repeatedly, or "iterated" by the same two players, the most effective strategy for each players is "tit-for-tat," for each to make an overture of cooperation, and after that respond in kind. This analysis supports disarmament initiatives and continuing the arms race. Tit-for-tat assumes that the "game" can be played repeatedly for an indefinite period.
Mathematical probability analysis offers insights that alter the character of the game. Since deterrence always has an instantaneous failure probability that can be represented by "p", the probability equation
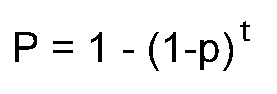
tells us that, over time (t) the failure probability of deterrence (P) approaches certainty. Since we have no empirical understanding of how long it will be before deterrence collapses into catastrophic nuclear war, the most rational assumption is "worst case," that its collapse is imminent. The imminent collapse of deterrence means that it's irrational to expect that the arms race "game" can be iterated indefinitely. This can be expressed by putting zeros into cell #4 in the game matrix; the utility of a "move" in which everyone dies can be represented by zero. Mathematical probability analysis therefore makes the game look like this:
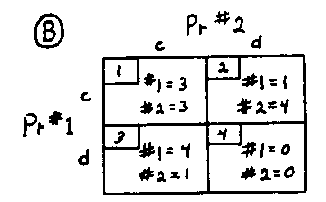
Matrix B isn't prisoners' dilemma. It's the model for a game of bluff called "chicken." In the classical example of chicken, two drivers place their cars on the center line of a highway and speed toward each other. If one swerves before the cars-collide, he or she is disgraced and supposedly loses the game.
But the arms race isn't exactly like chicken. While the drivers of the cars can see each other and estimate when they'll crash, we don't know when deterrence will collapse into nuclear war. It's as if the players of chicken couldn't see each other. We can call this game "blind chicken."
Is it rational to play blind chicken? The matrix shows that it isn't. For both "players".in cell #4, the rational choice is to migrate at once to cells 2 and 3, or 1. In all of these cells, the utilities for both "players" are greater than zero.
In this way, rational choice theory, game theory, and mathematical probability analysis combine to show why immediate, unconditional disarmament, and defense by nonviolent resistance - the pacifist policy - is the most scientific and rational course.
This article originally was published in the July 12, 1986 edition of the Midwest Pacifist Commentator. To encourage its greatest possible reproduction and distribution, it isn't copyrighted. Additional copies are available from:
Midwest Pacifist Center
5729 S. Dorchester Ave.
Chicago, IL 60637
U.S.A.
Tel: 773-324-0654
Fax: 773-324-6426
Email: blyttle@igc.org